Введение

Когда говорят "твердое тело", имеют ввиду состояние, в котором находится вещество. Большинство предметов, которые нас окружают и которыми мы пользуемся, представляют собой твердые тела. Поэтому естественно, что мы стараемся узнать возможно больше об их строении и свойствах. Оказывается, что большинство интересных свойств твердых тел определяется их электронным строением. Именно теорией электронной структуры занимается группа теории твердого тела кафедры квантовой механики.

Теория электронной структуры твердых тел - это очень широкая область, которая охватывает как кристаллические (идеальные кристаллы и кристаллы с дефектами), так и некристаллические (аморфные) твердые тела. Эта теория описывает и объясняет различные свойства твердых тел (механические, электрические, оптические, магнитные и другие) и разнообразные протекающие в объеме и на поверхности процессы, в том числе и такие специальные, как природа электрического сопротивления, фазовые переходы, магнитное упорядочение, рост кристаллов, дефектообразование при воздействии температуры и излучений, коррозию и многие другие. Несмотря на долгую историю развития физики твердого тела, природа некоторых явлений до сих пор не получила детального объяснения.

Последний пример - это явление высокотемпературной сверхпроводимости, которое было открыто Беднорцом и Мюллером в 1986 году. Термин "высокотемпературная" означает, что сверхпроводимость можно получить при использовании жидкого азота, который гораздо дешевле и доступнее жидкого гелия, необходимого при получении обычной сверхпроводимости. Поскольку с высокотемпературной сверхпроводимостью связывались большие надежды на техническое применение, это явление широко и интенсивно изучалось во всем мире и за прошедшие два десятилетия на эту тему написаны десятки тысяч статей. Были исследованы различные стороны этого явления, в частности, было установлено, что высокотемпературная сверхпроводимость связана с электронным состоянием кристаллических плоскостей, образованных ионами меди и кислорода, и что существенную роль здесь играют, так называемые, электронные дырки. Однако, механизм высокотемпературной сверхпроводимости до сих пор не выяснен и теория этого явления еще ждет своего открывателя. Это наиболее яркий пример нерешенной еще задачи физики твердого тела. Существует много других больших и малых нерешенных задач и физика твердого тела представляет широкое поле деятельности для теоретического исследования.

Такая ситуация определяется, конечно, сложностью решаемых задач. При этом, в отличие от многих других теорий, сложность здесь не в том, что неясно основное уравнение теории. В нерелятивистской теории электронной структуры твердых тел основное уравнение хорошо известно - это квантовое уравнение Шредингера для волновой функции:

Проблема состоит в сложности уравнения. Даже в самом простом случае оно сводится к уравнению в частных производных, число переменных (координатных и спиновых) в котором равно учетверённому числу электронов.

При этом слагаемые, описывающие кулоновское взаимодействие между электронами, не позволяют решить уравнение в конечном виде через элементарные функции. Для небольшого числа электронов можно пытаться решать это уравнение непосредственно с помощью компьютеров. В случае же твердого тела число переменных составляет 10²³ и, следовательно, без приближений здесь не обойтись.

Как правило, приближение связано с моделированием, физическим или математическим, то есть с заменой исходной физической системы такой ее моделью, которая допускает адекватное математическое описание. При моделировании выделяются основные характеристики физической системы или рассматриваемого процесса, а второстепенные детали отбрасываются, причем, делается это так, чтобы получались решабельные уравнения. Такое моделирование широко используется в теории твердого тела и, по существу, является неотъемлемой ее частью. Конечно, разделение на главные и второстепенные характеристики условно, и потому для одного и того же объекта можно получать модели разной степени сложности от простейших до весьма изощренных. Таким образом, в теории твердого тела можно сформулировать и простые задачи, и задачи средней степени сложности, и действительно сложные задачи.

Например, в теории твердого тела долгое время с успехом использовалась, и продолжает использоваться, так называемая, зонная схема, в которой энергетический спектр и свойства твердого тела описываются с помощью рассмотрения поведения одного электрона в периодическом поле. Однако, эта простая теория годится лишь в тех случаях, когда детали электрон- электронного взаимодействия не важны. В других случаях, например при описании экситонов, электрон-электронное взаимодействие оказывается существенным и приходится использовать более сложные многоэлектронные теории. К их числу можно отнести методы, основанные на приближении функционала плотности (автор W. Kohn - Нобелевский Лауреат 1999 года), на различных вариантах метода Хартри-Фока, широко используются модельные гамильтонианы Хаббарда или Гейзенберга. Они позволяют рассчитать электронное строение кристаллов, получить информацию о спектре возбуждений - экситонах, магнонах, поляронах, поляритонах, спинонах и т.д.

Немного истории

Теория многоэлектронных систем является традиционной тематикой кафедры квантовой механики (ранее кафедры теоретической физики). В течение многих лет нашей кафедрой заведовал академик В.А. Фок, который, в частности, является автором одного из основных методов теории многоэлектронных систем - метода Хартри-Фока. Уравнения этого метода, называемые уравнениями Хартри-Фока, были написаны из наглядных соображений профессором Кембриджского университета (Англия) Д. Хартри, и были математически строго выведены В.А. Фоком. При строгом выводе оказалось, что уравнения должны содержать специфические "обменные" слагаемые, которые не имеют классического аналога и потому не могут быть получены с помощью наглядных соображений. Метод Хартри-Фока играет фундаментальную роль в теории электронной структуры твердых тел. С одной стороны, многие приближенные методы получаются как результат упрощений, вводимых в метод Хартри-Фока. С другой стороны, он является основой при построении более точных методов.

Развитие теории твердого тела вообще и теории электронной структуры твердых тел на нашей кафедре связано с именами ныне покойных профессоров П.П. Павинского и М.И. Петрашень. Палладий Палладиевич Павинский инициировал развитие теории экситонов, направление, которое в работах его ученика А.Г. Жилича (и его учеников) превратилось в теорию оптических явлений в полупроводниках во внешних полях.

Мария Ивановна Петрашень с 1932 года работала под руководством В.А. Фока над теорией электронной структуры атомов. В 1956 году она со своими учениками перешла от изучения электронной структуры свободных атомов к изучению электронной структуры примесных атомов в кристалле, рассматривая их как атомы в поле, создаваемом кристаллическим окружением. Тем самым было положено начало развитию на кафедре многоэлектронной теории твердого тела, которое продолжается и по сей день. У М.И. Петрашень было много учеников (шесть учеников М.И. Петрашень защитили докторские диссертации и стали профессорами - И.В. Абаренков, А.А. Киселев, Н.Н. Кристофель, В.П. Смирнов, Е.Д. Трифонов, Р.А. Эварестов). Многие ученики М.И. Петрашень, а также другие бывшие сотрудники группы теории твердого тела, возглавили и возглавляют научные группы в других институтах. Профессор К.К. Ребане, который был аспирантом П.П. Павинского, в течение многих лет является президентом Академии наук Эстонии, профессор Е.Д. Трифонов заведовал кафедрой теоретической физики института им. Герцена. Профессор А.А. Киселев заведовал кафедрой теоретической физики в ЛИТМО, после его смерти этой кафедрой заведует профессор В.П. Смирнов. Ученик М.И. Петрашень профессор Р.А. Эварестов работал первым проректором нашего университета. Профессор Н.Н. Кристофель руководит группой в Институте физики АН Эстонии (Тарту), а профессор Б.С. Монозон, который был аспирантом А.Г. Жилича, - в кораблестроительном институте.

Наши достижения

Бывшими и ныне действующими сотрудниками группы теории твердого тела было получено много важных результатов, среди которых надо отметить следующие:

• Развита теория оптических явлений в полупроводниках во внешних полях. В приближении Хартри-Фока разработана теория электронной структуры ионных кристаллов.
• Построена теория электронной структуры точечных дефектов в ионных кристаллах.
• Группе принадлежит соавторство в методе псевдопотенциала, широко используемого в современной теории электронной структуры многоатомных систем.
• Разработаны новые методы в зонной теории твердых тел, основанные на применении теории групп. Развита теория симметрии нежестких молекул и кристаллов.
• Предсказан новый вид поверхностных экситонов.
• Разработана теория десорбции атомов с поверхности металла под действием внешнего поля.

Who is Who

В настоящее время в группе теории твердого тела работают три постоянных сотрудника: профессор И.В. Абаренков, доцент И.И. Тупицын и научный сотрудник С.Н. Загуляев. Неформально в группу также входят некоторые сотрудники ГОИ, ЛИТМО, ПИЯФ РАН, ПОМИ РАН. Кроме того, в группе работают аспиранты, магистранты и студенты.

Основные направления исследований

Одно из основных научных направлений, которым занимается большая часть группы, состоит в изучении электронного строения совершенных и несовершенных кристаллов, а также кластеров и молекул во внешних (кристаллических) полях. Для этого используются современные неэмпирические (многоконфигурационные методы, метод функционала плотности) и полуэмпирические методы квантовой механики. Рассматриваются следующие задачи:

• Определение локальных характеристик атомов в кристаллах - зарядов, магнитных моментов, кристаллографических валентностей; особенностей зонной структуры, неспаренной спиновой плотности, характера химической связи и т.д.
• Релятивистские многоконфигурационные расчеты атомов, молекул и малых кластеров. Генерация релятивистских псевдопотенциалов. Расчеты констант сверхтонких расщеплений, электронных плотностей на ядре, констант ЯМР, изотопических и химических сдвигов жестких рентгеновских линий.
• Построение нерелятивистских и релятивистских эффективных потенциалов остова (псевдо-потенциалов и сепарабельных псевдопотенциалов).
• Исследование спиновых систем - цепочек и плоскостей, в частности, их антиферромагнитное упорядочение. Здесь не только рассматриваются общепринятые модели, но выводятся и исследуются более точные, а потому и более сложные, нелинейные, уравнения для спиновой волновой функции.
• Квантовая теория магнетизма и высокотемпературная сверхпроводимость.

доктор физико-математических наук, профессор

• Абаренков Игорь Васильевич

Заслуженный деятель науки Российской Федерации
Fellow of the Institute of Physics (UK)
возглавляет направление "Теория твердого тела"

В современной науке и технике необходимо знать не только усредненные (как это было раньше), но и детальные характеристики и детальное строение сложных твердотельных систем. В частности, сейчас на смену микроэлектронике приходит наноэлектроника, рабочие элементы которой содержат всего несколько десятков атомов, причем атомы этих рабочих элементов не образуют изолированные группы, а находятся во взаимодействии с атомами основы. Таким образом здесь приходится исследовать на атомарном уровне свойства системы, которая содержит огромное число атомов (порядка 10²⁰). В силу сложности рассматриваемых систем использование одних экспериментальных методов исследования не позволяет получить всю необходимую информацию о системе и здесь на помощь приходит теория.

Интересующие нас свойства сложной системы определяются ее электронной структурой, то есть строением электронных оболочек системы, причем, в нашем случае, электронную структуру системы надо знать с высокой степенью точности. Теория позволяет, в принципе, найти электронную структуру любой многоэлектронной системы. Для этого надо рассчитать волновую функцию этой системы, решив соответствующее уравнение Шредингера, которое представляет собой дифференциальное уравнение второго порядка в частных производных. Однако, непосредственное решение дифференциального уравнения в частных производных возможно, если уравнение содержит небольшое число переменных (порядка пяти-десяти). В нашем же случае, число переменных огромно, оно в десятки раз больше числа атомов в системе. В квантовой теории разработаны приближенные методы расчета волновых функций многоэлектронных систем, которые позволяют найти с приемлемой степенью точности волновую функцию системы, содержащей несколько десятков атомов. Таким образом, затратив довольно большое количество компьютерного времени, можно определить электронную структуру изолированного рабочего элемента наноэлектронного устройства. Однако, как уже было сказано выше, эти рабочие элементы системы не являются изолированными, а образуют, так называемый кластер, состоящий из связанных между собой атомов, которые взаимодействуют не только друг с другом, но и с остальными атомами большой системы. Таким образом, возникает задача нахождения электронной структуры кластера, который является малой частью большой системы. Именно этой задачей и занимается наша группа.

Метод, используемый нашей группой состоит в том, чтобы рассматривать не изолированный кластер, а поместить этот кластер в поле окружения, которое описывало бы влияние всех остальных атомов системы на данный кластер. Проблема состоит в построение поля окружения. Решение этой проблемы для систем с чисто ионными связями является сравнительно простым. В случае чисто ионных систем можно провести границы между ионами, часть ионов отнести к кластеру, остальные ионы отнести к окружению, и построить потенциал окружения как сумму электростатического потенциала окружения и обменно-корреляционных потенциалов ионов окружения, соседних с ионами кластера. Гораздо более сложной является проблема построения поля окружения для систем с ковалентными связями. Здесь при непосредственном разделении системы на кластер и окружение разрываются ковалентные связи между атомами кластера и атомами окружения. В работах нашей группы было предложено включать в кластер не только атомы, но и связи между кластером и окружением. При этом поле окружения надо строить так, чтобы связи кластера в поле были такими же, как и связи кластера с окружением.

Рассмотрим в качестве примера примесь атома железа в кристалле кремния. В этом случае наименьшим кластером будет ион железа и четыре связи железа с соседними атомами кремния. При построении поля окружения надо реальные четырехвалентные атомы кремния заменить одновалентными атомами псевдокремния, но так, чтобы связь псевдокремния с железом была бы такой же как и связь настоящего кремния. В данном случае задача сводится к построению потенциала псевдокремния, восстанавливающего оборванные ковалентные связи.

В нашей группе разработан строгий метод (в рамках метода Хартри-Фока) построения поля окружения, восстанавливающего оборванные связи в общем случае. Для этого предложено использовать сепарабельный потенциал (конечно-мерный оператор) и разработан метод построения сепарабельного потенциала описывающего поле окружения. Как правило, точный метод решения задачи требует очень большого компьютерного времени. Не является исключением и сепарабельный потенциал окружения. Поэтому в настоящее время в группе производится поиск и разработка более простых приближенных потенциалов, которые позволяли бы эффективно и сравнительно быстро решать задачу определения электронной структуры кластера, являющегося частью большой системы. При этом используются как строгие математические методы, так и приемы моделирования, основанные на качественных соображениях и использующие накопленный опыт расчета простых модельных систем.

доктор физико-математических наук, профессор

• Тупицын Илья Игоревич

В нашей группе проводятся работы по теоретическому изучению электронной структуры идеальных кристаллов и кристаллов с дефектами. Основным методом, который мы используем в настоящее время, для исследования зонной структуры кристаллов является метод функционала плотности (ТФП). Один из основателей метода ТФП В. Кон получил нобелевскую премию по химии в 1998 году. Первые работы, написанные В.Коном в соавторстве с П.Хоэнбергом и Л.Дж.Шемом, были опубликованы в 1964 и 1965 годах соответственно. В этих работах было показано, что для получения одноэлектронной плотности и полной энергии основного состояния системы достаточно решить уравнения Кона-Шема

За последние 40 лет, прошедших с тех пор был достигнут громадный прогресс в изучении различных свойств кристаллов методом функционала плотности, чему в решающей степени способствовало бурное развитие вычислительной техники. Современный уровень развития метода ТФП, в отличие от других неэмпирических методов исследования конденсированного вещества, позволяет рассматривать системы содержащие огромное количество атомов, например, кристаллы, содержащие 100 - 1000 атомов в элементарной ячейке.

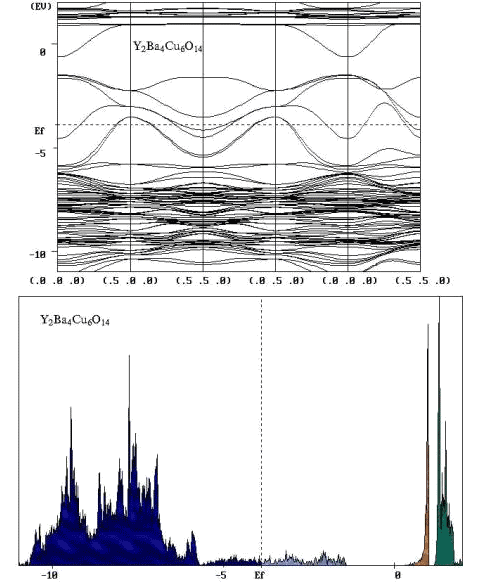
В наших работах метод ТФП используется в сочетании с современной теорией псевдопотенциала и с использованием простого и удобного базиса плоских волн. Мы исследуем зонную структуру кристаллов, плотности электронных состояний, проводим работы по теоретическому определению координат атомов в элементарной ячейке и т.д. Многие физические и химические свойства твердых тел описываются локальными электронными состояниями. Для описания локальных свойств, таких как заряды на атомах, атомные заселенности, валентности атомов, порядки химических связей и т.д. базис плоских волн, делокализованных по всему кристаллу, является неудобным. Нами разработана техника проектирования делокализованных (Блоховских состояний) на пространство атомо-подобных орбиталей или функций Ванье.

В сотрудничестве с экспериментальной рентгено-спектральной лабораторией мы проводим работы по теоретическому изучению рентгеновских спектров твердых тел. С этой целью мы развиваем специальную теорию, позволяющую рассчитывать вероятности рентгеновских переходов в кристаллах. Теоретическая и экспериментальная рентгеновские спектроскопии позволяют напрямую изучать состояние атомов в кристаллах.

При изучении электронной структуры кристаллов методом ТФП или другими неэмпирическим методами часто необходимо начинать с расчета волновых функций атомов и простых молекул, входящих в состав твердого тела. Если атомы достаточно тяжелые, т.е. имеют заряд ядра более 30, необходимо учитывать релятивистские эффекты. Дело в том, что электроны в области атомного остова для больших Z движутся со скоростями, сравнимыми со скоростью света и поэтому учет релятивистских эффектов становится необходимым. В группе накоплен большой опыт проведения релятивистских расчетов атомов и молекул, основанный на численном решении многоэлектронного уравнения Дирака-Брейта:

где четырех рядные матрицы Дирака и выражаются через двурядные матрицы Паули . Для получения приближенных решений многоэлектронного уравнения Дирака используются методы ТФП, Хартри-Фока, могоконфигурационный метод Хартри-Фока и для молекул - многоконфигурационный метод валентных схем. Последние два метода дают возможность учитывать корреляционные эффекты, влияние которых на электронную структуру атомов, молекул и твердых тел очень велико. Роль релятивистских эффектов может быть оценена, если сравнить результаты релятивистских расчетов с аналогичными расчетами, в которых скорость света устремить к бесконечности, т.е. перейти к так называемому нерелятивистскому пределу. В нерелятивистском пределе результаты должны совпадать с результатами нерелятивистских расчетов, основанных на решении нерелятивистского уравнения Шредингера. Такое сравнение предоставляет хороший тест для проверки правильности полученных результатов.

После получения атомных и молекулярных волновых функций нами строятся релятивистские (или нерелятивистские) псевдопотенциалы, знание которых необходимо для проведения расчетов электронной структуры кристаллов. К сожалению, в настоящее время нет возможности последовательно или, как говорят, из первых принципов учесть корреляционные эффекты в расчетах электронной структуры кристаллов в рамках многоконфигурационного метода Хартри-Фока, также, как это делается для атомов и молекул. Развитие соответствующих методов является важнейшей задачей ближайшего будущего.

научный сотрудник

• Загуляев Сергей Николаевич

Одной из наиболее сложных проблем теории твердого тела является описание кооперативных явлений в кристаллах, таких как магнетизм, сверхпроводимость, сегнето-, пиро- и пьезоэлектрические эффекты, разного рода магнетоэластические и магнетооптические фазовые переходы. Законченных и последовательных квантовых теорий для многих из этих феноменов не удается создать на протяжении практически целого века. Ключом к пониманию природы этих феноменов является детальное изучение электронного строения таких кристаллов. В нашей группе проводятся численные расчеты электронной структуры и физических свойств идеальных кристаллов высокотемпературных сверхпроводников (ВТСП), магнитных диэлектриков, а также, этих кристаллов содержащих примеси. Для этого используется неограниченный по спину метод Хартри-Фока-Рутана:

и различные полуэмпирические методы на его основе. Однако для описания необычных физических свойств этих кристаллов недостаточно одного умения рассчитывать их электронную структуру. Необходимо научиться корректно интерпретировать результаты расчетов, чтобы извлекать из них информацию, о физических свойствах (а в перспективе - и предсказывать их). Для сравнения с экспериментальными данными часто требуется проследить за изменением какого либо свойства кристалла в зависимости от температуры, давления, внешних полей, концентрации примесей. Для этого приходится проводить целые серии расчетов одного и того же кристалла, при разных значений изменяемого параметра. Так, например, вычисление полной электронной энергии кристалла для разных взаимных ориентаций магнитных моментов ионов (s_j), входящих в его состав, позволяет вычислить интегралы эффективных обменных взаимодействий (J_ij) между ними и зависимость J_ij от расстояния. В дальнейшем, эти обменные интегралы используются в качестве эмпирических параметров в различного рода модельных спиновых гамильтонианах (гамильтониан Изинга, Гейзенберга, XXX-,XXZ-,XYZ-модели математической физики), которые, в самом общем виде, могут быть записаны в виде суммы билинейных форм:

Для успешного применения подобных гамильтонианов при описании физических свойств необходимо, в первую очередь, выделить в кристалле модельную подсистему, что невозможно без предварительного исследования зонной структуры. При корректном выборе такой модельной подсистемы и при удачно подобранных эмпирических параметрах удается получить качественное описание наблюдаемых свойств в виде достаточно компактных аналитических выражений. Так, например, при исследовании кристаллов ВТСП допированных магнитными примесями удается описать зависимость характеристической температуры Кюри/Вейсса ( или ) от концентрации примесей и концентрации носителей тока в рамках модели опосредованного взаимодействия магнитных моментов примесей через газ свободных носителей заряда - RKKY-взаимодействие. Результаты расчетов (), для 1D-линейной цепочки, 2D-квадратной и 3D-кубической решеток, были выполнены для случайного, периодического и однородного распределения атомов магнитных примесей по узлам решетки. Они представлены на рисунке слева.

научный сотрудник

• Кузнецов Владимир Георгиевич

В сотрудничестве с проф. И.В.Абаренковым и проф. И.И.Тупицыным я занимаюсь изучением электронной структуры молекул, кластеров, кристаллов и стекол. Мы используем неэмпирические, так называемые, "ab initio" методы расчета, такие как метод Хартри-Фока, Дирака-Фока, многоконфигурационный метод самосогласовнного поля, метод функционала плотности и т.д. Особое внимание уделяется изучению дефектов в кристаллах, а также cложным квазимолекулярным комплексам, которые играют определяющую роль во многих важных физико-химических процессах, таких как адсорбция, катализ, фотохромные процессы в кристаллах и стеклах и т.д. Для систем, содержащих тяжелые атомы расчеты проводятся с использованием эффективных потенциалов остова и псевдопотенциалов.

Существует много других больших и малых нерешенных задач и физика твердого тела представляет широкое поле деятельности для теоретического исследования.