Квантовый хаос
В классической механике движение называется регулярным, или устойчивым, если малому изменению начальных условий соответствует отклонение траектории от начальной, максимум линейно нарастающее во времени. Однако в подавляющем большинстве случаев движения с более чем одной степенью свободы (только такие системы рассматриваются далее) возмущение траектории нарастает экспоненциально. Движение называется тогда хаотическим; детальное предсказание отдаленного будущего таких систем невозможно. С другой стороны, в квантовой механике эволюция волновой функции, описываемая нестационарным уравнением Шредингера, всегда устойчива. Роль частот в ней играют разности энергий квантовых уровней, которые вещественны, и, следовательно, не могут привести к экспоненциально нарастающим компонентам в решении уравнения Шредингера. Отсюда проблема "квантового хаоса": к каким наблюдаемым последствиям на квантовом уровне ведет хаотический характер соответствующего классического движения?
Наиболее наглядно различие между двумя группами систем в квантовой постановке проявляется в статистике их высоковозбужденных уровней энергии. Простейшей характеристикой
является распределение интервалов энергии между двумя ближайшими уровнями. В спектрах классически регулярных систем функция распределения
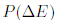 максимальна при
максимальна при 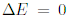 и экспоненциально спадает с ростом
и экспоненциально спадает с ростом
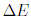 : уровни предпочитают группироваться друг с другом. В хаотических системах, напротив, уровни отталкиваются:
: уровни предпочитают группироваться друг с другом. В хаотических системах, напротив, уровни отталкиваются:
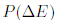 равна нулю при
равна нулю при 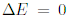 , далее растет по степенному закону, достигая максимума при
значениях, близких к среднему интервалу между уровнями
, далее растет по степенному закону, достигая максимума при
значениях, близких к среднему интервалу между уровнями 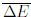 , а затем быстро убывает. Более сложной статистической
характеристикой является спектральная двухточечная корреляционная функция
, а затем быстро убывает. Более сложной статистической
характеристикой является спектральная двухточечная корреляционная функция 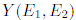 . Это отклонение плотности вероятности найти один
уровень энергии в точке
. Это отклонение плотности вероятности найти один
уровень энергии в точке 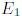 , а другой в точке
, а другой в точке 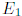 , от произведения соответствующих
средних плотностей. Уровни энергии полностью нескоррелированы:
, от произведения соответствующих
средних плотностей. Уровни энергии полностью нескоррелированы: 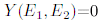 , в классически регулярных системах и скоррелированы в
хаотических системах. Чаще вместо
, в классически регулярных системах и скоррелированы в
хаотических системах. Чаще вместо 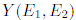 используется ее Фурье-преобразование по отношению к разности энергий
используется ее Фурье-преобразование по отношению к разности энергий
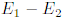 , так называемый спектральный формфактор
, так называемый спектральный формфактор 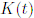 .
.
В 60 - 80х годы прошлого столетия было осознано, что спектры хаотических систем не только отличаются от спектров классически регулярных систем, но и являются
универсальными: распределение энергетических интервалов, спектральная корреляционная функция и формфактор совпадают у самых разных физических систем, принадлежащих к
одному и тому же "классу универсальности". Главными из этих классов (Дайсон, 1962) являются "ортогональный" (системы без спина или целым спином, допускающие обращение
времени); "унитарный" (обращение времени не допускается в силу, например, наличия внешнего магнитного поля) и "симплектический" (системы с полуцелым спином при наличии
обращения времени); недавно были установлены более экзотические классы. Такие же статистические характеристики встречаются в области, не имеющей очевидного отношения к
физике, а именно, в теории спектров случайных эрмитовских матриц (RMT - random matrix theory); распределение унитарного и ортогонального типа наблюдается в ансамблях
комплексных и вещественных матриц соответственно. При сопоставлении статистических характеристик предполагается переход к безразмерным переменным: энергии следует
выражать в единицах среднего энергетического интервала 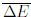 , а вместо времени в формфакторе использовать аргумент
, а вместо времени в формфакторе использовать аргумент
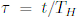 , где
, где 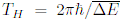 - "время Гейзенберга", минимальное время измерения, необходимое для того,
чтобы разрешить спектральный интервал
- "время Гейзенберга", минимальное время измерения, необходимое для того,
чтобы разрешить спектральный интервал 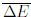 . Приведем для иллюстрации формфакторы унитарного
. Приведем для иллюстрации формфакторы унитарного
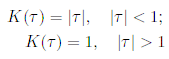
и ортогонального классов
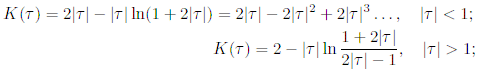
обращаем внимание на странную смену поведения при 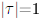 и на то, что при малых
и на то, что при малых 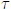 ортогональный формфактор вдвое больше унитарного. В виде предположения универсальность статистических спектральных свойств систем с хаотическим классическим поведением
была провозглашена в работе Бохигаса, Джаннони и Шмита ("гипотеза BGS") в 1984 году.
ортогональный формфактор вдвое больше унитарного. В виде предположения универсальность статистических спектральных свойств систем с хаотическим классическим поведением
была провозглашена в работе Бохигаса, Джаннони и Шмита ("гипотеза BGS") в 1984 году.
Доказательство BGS потребовало более 20 лет и было начато Майклом Берри (1985), который предложил использовать квазиклассическое представление для формфактора. Оно следует из знаменитой формулы Гутцвиллера для квантования уровней энергии хаотических систем и имеет вид двойной суммы по классическим периодическим орбитам системы,
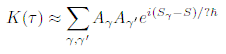
Здесь 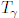 и
и 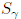 период и действие классической орбиты
период и действие классической орбиты
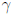 . В квазиклассическом пределе орбиты, участвующие в сумме, имеют действия, гигантские по сравнению с
. В квазиклассическом пределе орбиты, участвующие в сумме, имеют действия, гигантские по сравнению с
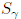 . Поэтому подавляющее большинство пар имеют огромные, случайно распределенные, фазы; их сумма взаимно уничтожается.
Существенный вклад могут вносить пары, у которых разность действий порядка
. Поэтому подавляющее большинство пар имеют огромные, случайно распределенные, фазы; их сумма взаимно уничтожается.
Существенный вклад могут вносить пары, у которых разность действий порядка 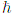 или меньше. Очевидными кандидатами являются
"диагональные пары", т.е.
или меньше. Очевидными кандидатами являются
"диагональные пары", т.е. 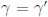 , когда разность действий точно равна нулю. Сумма вкладов таких пар приводит
к выражению
, когда разность действий точно равна нулю. Сумма вкладов таких пар приводит
к выражению 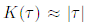 . Если в системе допустимо обращение времени, направление движения по каждой орбите может быть
заменено на противоположное. Число диагональных пар тогда удваивается, и мы получаем
. Если в системе допустимо обращение времени, направление движения по каждой орбите может быть
заменено на противоположное. Число диагональных пар тогда удваивается, и мы получаем 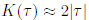 . Тем самым удалось
объяснить поведение формфактора при малых временах для двух главных классов универсальности.
. Тем самым удалось
объяснить поведение формфактора при малых временах для двух главных классов универсальности.
Следующий шаг был сделан в работе Зибера и Рихтера (2001). Длинная классическая периодическая орбита в финитном хаотическом движении многократно пересекает саму себя;
часть таких самопересечений происходит с малыми углами (Рис. 1A). С каждым таким самопересечением при наличии обращения времени связано существование орбиты-"партнера":
партнер практически совпадает с исходной орбитой всюду, кроме области пересечения, которое заменяется на квазипересечение; направление движения по части орбиты меняется
на противоположное (Рис. 1B). Возможность такого пересоединения кусков орбиты в области пересечения нетривиальна и требует неустойчивости движения. Вычисления вклада
пар-партнеров продвигает нас на один шаг в разложении ортогонального формфактора, 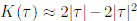 .
.

Рис 1. A - топологическая схема длинной периодической орбиты, у которой выделено одно ("активное") из множества ее самопересечений; B - орбита-партнер, практически совпадающая с А всюду, кроме окрестности активного самопересечения (замененного на квазипересечение).
Обобщение этого метода было сделано в работах группы авторов в 2002 - 2007гг (Браун, Мюллер, Хааке, Хойслер, Эссен - Санкт-Петербург). Ключевым здесь является понятие l - сближения (l - encounter) - относительно кратковременная, в силу экспоненциальной неустойчивости, ситуация, когда l участков периодической орбиты одновременно подходят друг к другу аномально близко, имея при этом почти параллельные или антипараллельные скорости. Сближение делит орбиту на l определенным образом соединенных частей. Важность сближений связана с тем, что наряду с исходной, существует еще l! - 1 периодических орбит-партнеров, состоящие практически из тех же l частей, по-другому соединенных внутри сближения. Таким образом, сближения являются своеобразными переключателями хаотической динамики. Действие всех орбит-партнеров будет тем более близким друг к другу. чем теснее подходят друг к другу участки орбиты в сближении, т.е. чем более нежная хирургическая операция необходима для пересоединения частей орбиты внутри сближения.

Рис 2. Орбита с двумя активными сближениями, l = 2, 3 (черная линия) и ее партнер (красная линия).
Следует учесть, что пересоединения внутри сближений могут привести к распаду орбиты на несколько несвязанных периодических орбит, суммарное действие которых близко к
действию исходной орбиты, т.е. к образованию т.н. псевдоорбиты, которая не может участвовать в качестве партнера в формуле для формфактора. Далее, партнеры могут
отличаться друг от друга пересоединением в нескольких сближениях (Рис. 2), а топология соединения сближений частями орбиты может быть различной. Все это крайне осложняет
подсчет вклада орбит-партнеров, которое тем не менее удалось произвести аналитически. В результате как при наличии, так и в отсутствие обращения времени воспроизводится
результат RMT для 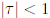 ; в частности, в унитарном случае выживает лишь вклад диагональных пар, а суммарный
вклад всех пар из нетождественных орбит сокращается.
; в частности, в унитарном случае выживает лишь вклад диагональных пар, а суммарный
вклад всех пар из нетождественных орбит сокращается.
Расчет формфактора для 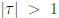 был произведен в самое последнее время (2007). Первичным объектом расчета при
этом являлясь двухточечная корреляционная функция, для которой было использовано квазиклассическое представление, отличающееся от общепринятого. Результат снова сводится
к суммированию по парам орбит-партнеров, получаемых переключениями внутри сближений; интересно, что вклад вносят не только пары орбит, но и псевдоорбит.
был произведен в самое последнее время (2007). Первичным объектом расчета при
этом являлясь двухточечная корреляционная функция, для которой было использовано квазиклассическое представление, отличающееся от общепринятого. Результат снова сводится
к суммированию по парам орбит-партнеров, получаемых переключениями внутри сближений; интересно, что вклад вносят не только пары орбит, но и псевдоорбит.
Разработанная методика оказывается полезной не только в задачах спектральной статистики, но и в т.н. баллистических транспортных задачах физики твердого тела. Грубой
моделью может служить прохождение слабого электронного пучка через полость достаточно сложной формы, снабженной несколькими небольшими отверстиями; электроны влетают в
полость по одному через входное отверстие, странствуют внутри нее, упруго отражаясь от стенок, а затем вылетают через другое либо то же самое отверстие. Рассчитываемой
величиной является проводимость (какой процент электронов вылетает через выходное отверстие, а какой обратно через вход); флюктуации проводимости при изменении скорости
электронов и при включении внешнего магнитного поля; дробовой шум (временные флюктуации электронного тока) и т.д. Все эти величины могут быть представлены в виде суммы
вкладов пар (или четверок) классических траекторий; существенного вклада можно ожидать в случаях, когда разность действий компонент пар (или четверок) имеет порядок
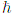 или меньше. Результат получается суммированиям по парам (четверкам) незамкнутых траекторий-партнеров,
соединяющих входное и выходное отверстия и различающихся пересоединениями частей траектории внутри сближений.
или меньше. Результат получается суммированиям по парам (четверкам) незамкнутых траекторий-партнеров,
соединяющих входное и выходное отверстия и различающихся пересоединениями частей траектории внутри сближений.
Теория квантового хаоса еще далека до завершения. Кажется вероятным, что помимо сближений, существует другой, еще неизвестный, механизм корреляции действий периодических
орбит, учет которого позволил бы получить формфактор для всех времен непосредственно из квазиклассического представления Берри (мы сейчас умеем это делать сложным окольным
методом). На эту мысль наталкивает ситуация с нулями дзета-функции Римана, мнимая часть которых почему-то подчиняется той же статистике, что и уровни энергии унитарного
класса; роль периодических орбит в этом случае играют простые целые числа, а указанная корреляция известна и составляет содержание т.н. гипотезы Харди-Литтлвуда в теории
чисел. Обнаружение такого механизма в физических задачах хаотической динамики явилось бы большим достижением. Менее масштабным, но тем не менее интересным было бы
исследование спектральной статистики в системах с т.н. арифметическим хаосом; не вдаваясь в детали, укажем, что для таких систем характерно вырождение действия
периодических орбит, что должно приводить к переформулировке диагонального приближения и понятия партнерства. В транспортных задачах не вполне ясно, как физика задачи
зависит от типичной ширины отверстий 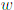 ; ключевым параметром при этом является соотношение между
; ключевым параметром при этом является соотношение между
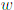 и
и 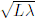 где L - размер
полости,
где L - размер
полости, 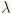 - длина волны Де Бройля.
- длина волны Де Бройля.
Активные исследования по теории квантового хаоса ведутся на кафедре П.А. Брауном.